Programs
This is where I release all my programs for TI-Nspire™. Some are also available in other sites, but this page is the first place to look if you want an updated version.
If you don't have TI-Nspire you can download the trial version of the computer software from Texas Instruments' website and install it on your computer. It's valid for 30 days and allows you to explore its potential freely, namely testing the programs listed below.
Remark: All files in this section were built on version 1.7 of TI-Nspire software. In order to download and install them you first need to update your TI-Nspire. You can download the latest version from TI's website.
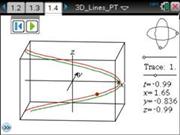
3D Lines is a document that allows plotting up to 3 parametric curves in 3 dimensional space. It also allows rotation and graph trace.
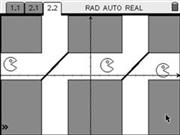
This document is inspired on the Ants program for TI-83 Plus and TI-84 Plus. IT's a mathematical game: from the white path on the screen find out which function allows you to catch pacmen while avoiding the walls and obstacles.
It has 3 difficulty levels, allowing a fun approach of the study of rational functions and asymptotes (vertical, horizontal and slant).

A graphical Periodic Table with all information about the 118 elements currently known to man. Includes a graphical interface, displays data from each element in a spreadsheet, plots atomic properties vs. atomic number and has functions to determine names, symbols and masses from any element.
Available in English, Portuguese, French, Spanish and German.
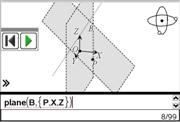
Nspir3D is a 3D geometry application for TI-Nspire. It allows creating points, lines and planes as well as perpendicular and parallel objects.
The constructions can be rotated in space or animated. It also features zoom functions to enlarge or reduce the construction.
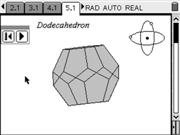
This collection of TNS files shows a 3D viewer of several common polyhedra. Each polyhedron can be freely rotated or animated. The collection (4 TNS files) includes: all platonic polyhedra, pyramids, prisms and also a small surprise.
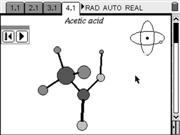
A collection of TNS files (3 files) with the structure of several molecules in 3D. Each molecule can be rotated freely or animated. These files include both inorganic and organic molecules, from water to benzene.
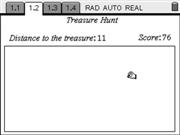
A simple yet fun game for TI-Nspire. The goal is to find a hidden treasure. The only help we have is a metal detector that tells us how far the treasure is (but not the direction). The faster we find it the higher our score!

This file is a library with programs to calculate molecular masses and to balance chemical equations, amongst other useful functions.
Once installed on the MyLib folder the programs of this library will be accessible from any other document, via the Catalog.

This document is a library that allows unit conversion and universal constants in a way similar to the one used by TI-Nspire CAS.
TI-Nspire CAS already includes this functionality and for that reason this library isn't needed.

This file can be downloaded to the Mylib folder on a TI-Nspire handheld and allows solving 2nd degree equations and systems of linear equations in a simpler way than the one available on TI-Nspire's operating system.
Not needed on TI-Nspire CAS.

A personal organizer for your TI-Nspire. It features a graphical calendar, appointment list and phonebook.

A perpetual calendar on TI-Nspire. Just select the month and year and the calendar will be automatically presented on a geometry page.
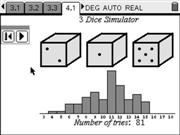
This program simulates successive dice rolls and displays the histogram of frequencies of each result, updating it in realtime.
The document has three different simulators, of 1, 2 and 3 dice respectively. Data from each simulator is stored independently.
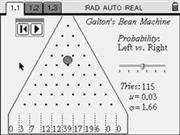
Galton's bean machine is a probabilistic simulation where a disc is released on a triangular grid of pins. Each time the disc hits a pin it can either fall to the left or to the right. Where will the disc fall after 10 levels of pins?

Buffon's needle is an experiment developed in the 18th century as a way to determine an approximation to the value of Pi.
In a sheet of paper where evenly spaced paralel lines are drawn a needle of a certain size is dropped. What's the probability that the needle crosses (at least) one line?
